control.lqe

control.lqe(A, G, C, QN, RN[, NN])[source]

Linear quadratic estimator design (Kalman filter) for continuous-time systems. Given the system

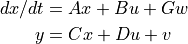
$dx/dt &= Ax + Bu + Gw \\ y &= Cx + Du + v$

with unbiased process noise w and measurement noise v with covariances

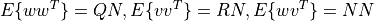
$E\{w w^T\} = QN, E\{v v^T\} = RN, E\{w v^T\} = NN$

The lqe() function computes the observer gain matrix L such that the stationary (non-time-varying) Kalman filter

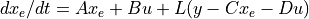
$dx_e/dt = A x_e + B u + L(y - C x_e - D u)$

produces a state estimate x_e that minimizes the expected squared error using the sensor measurements y. The noise cross-correlation NN is set to zero when omitted.

The function can be called with either 3, 4, 5, or 6 arguments:

L, P, E = lqe(sys, QN, RN)
L, P, E = lqe(sys, QN, RN, NN)
L, P, E = lqe(A, G, C, QN, RN)
L, P, E = lqe(A, G, C, QN, RN, NN)

where sys is an LTI object, and A, G, C, QN, RN, and NN are 2D arrays or matrices of appropriate dimension.

Parameters

A (2D array_like) – Dynamics, process noise (disturbance), and output matrices
G (2D array_like) – Dynamics, process noise (disturbance), and output matrices
C (2D array_like) – Dynamics, process noise (disturbance), and output matrices
sys (LTI (StateSpace or TransferFunction)) – Linear I/O system, with the process noise input taken as the system input.
QN (2D array_like) – Process and sensor noise covariance matrices
RN (2D array_like) – Process and sensor noise covariance matrices
NN (2D array, optional) – Cross covariance matrix. Not currently implemented.
method (str, optional) – Set the method used for computing the result. Current methods are ‘slycot’ and ‘scipy’. If set to None (default), try ‘slycot’ first and then ‘scipy’.

Returns

L (2D array) – Kalman estimator gain
P (2D array) – Solution to Riccati equation

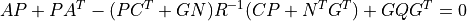
$A P + P A^T - (P C^T + G N) R^{-1} (C P + N^T G^T) + G Q G^T = 0$
E (1D array) – Eigenvalues of estimator poles eig(A - L C)

Notes

If the first argument is an LTI object, then this object will be used to define the dynamics, noise and output matrices. Furthermore, if the LTI object corresponds to a discrete time system, the dlqe() function will be called.

Examples

>>> L, P, E = lqe(A, G, C, QN, RN)                          
>>> L, P, E = lqe(A, G, C, Q, RN, NN)                       