control.dlqe

control.dlqe(A, G, C, QN, RN[, N])[source]

Discrete-time linear quadratic estimator (Kalman filter).

Given the system

$x[n+1] &= Ax[n] + Bu[n] + Gw[n] \\ y[n] &= Cx[n] + Du[n] + v[n]$

with unbiased process noise w and measurement noise v with covariances

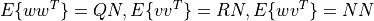
$E\{w w^T\} = QN, E\{v v^T\} = RN, E\{w v^T\} = NN$

The dlqe() function computes the observer gain matrix L such that the stationary (non-time-varying) Kalman filter

$x_e[n+1] = A x_e[n] + B u[n] + L(y[n] - C x_e[n] - D u[n])$

produces a state estimate x_e[n] that minimizes the expected squared error using the sensor measurements y. The noise cross-correlation NN is set to zero when omitted.

Parameters

A, G, C2D array_like: Dynamics, process noise (disturbance), and output matrices.
QN, RN2D array_like: Process and sensor noise covariance matrices.
NN2D array, optional: Cross covariance matrix (not yet supported).
methodstr, optional: Set the method used for computing the result. Current methods are ‘slycot’ and ‘scipy’. If set to None (default), try ‘slycot’ first and then ‘scipy’.

Returns

L2D array: Kalman estimator gain.
P2D array: Solution to Riccati equation.

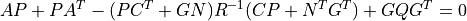
$A P + P A^T - (P C^T + G N) R^{-1} (C P + N^T G^T) + G Q G^T = 0$
E1D array: Eigenvalues of estimator poles eig(A - L C).