control.flatsys.BezierFamily

class control.flatsys.BezierFamily(N, T=1)[source]

Bezier curve basis functions.

This class represents the family of polynomials of the form

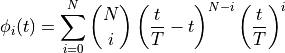
$\phi_i(t) = \sum_{i=0}^N {N \choose i} \left( \frac{t}{T} - t \right)^{N-i} \left( \frac{t}{T} \right)^i$

Parameters

Methods

`__call__`	Evaluate the ith basis function at a point in time.
`eval`	Compute function values given the coefficients and time points.
`eval_deriv`	Evaluate kth derivative of ith basis function at time t.
`var_ncoefs`	Get the number of coefficients for a variable.

__call__(i, t, var=None)[source]: Evaluate the ith basis function at a point in time.

eval(coeffs, tlist, var=None)[source]

Compute function values given the coefficients and time points.

Parameters

coeffsarray: Basis function coefficient values.
tlistarray: List of times at which to evaluate the function.
varint or None, optional: Number of independent variables represented using the basis. If None, then basis represents a single variable.

Returns

eval_deriv(i, k, t, var=None)[source]

Evaluate kth derivative of ith basis function at time t.

See BasisFamily.eval_deriv for more information.

var_ncoefs(var)[source]

Get the number of coefficients for a variable.

Parameters

Returns