control.bode_plot
- control.bode_plot(data, omega=None, *fmt, ax=None, omega_limits=None, omega_num=None, plot=None, plot_magnitude=True, plot_phase=None, overlay_outputs=None, overlay_inputs=None, phase_label=None, magnitude_label=None, display_margins=None, margins_method='best', legend_map=None, legend_loc=None, sharex=None, sharey=None, title=None, **kwargs)[source]
Bode plot for a system.
Plot the magnitude and phase of the frequency response over a (optional) frequency range.
- Parameters
data (list of FrequencyResponseData or LTI) – List of LTI systems or
FrequencyResponseDataobjects. A single system or frequency response can also be passed.omega (array_like, optoinal) – List of frequencies in rad/sec over to plot over. If not specified, this will be determined from the proporties of the systems. Ignored if data is not a list of systems.
*fmt (
matplotlib.pyplot.plot()format string, optional) – Passed to matplotlib as the format string for all lines in the plot. The omega parameter must be present (use omega=None if needed).dB (bool) – If True, plot result in dB. Default is False.
Hz (bool) – If True, plot frequency in Hz (omega must be provided in rad/sec). Default value (False) set by config.defaults[‘freqplot.Hz’].
deg (bool) – If True, plot phase in degrees (else radians). Default value (True) set by config.defaults[‘freqplot.deg’].
display_margins (bool or str) – If True, draw gain and phase margin lines on the magnitude and phase graphs and display the margins at the top of the graph. If set to ‘overlay’, the values for the gain and phase margin are placed on the graph. Setting display_margins turns off the axes grid.
margins_method (str, optional) – Method to use in computing margins (see
stability_margins()).**kwargs (
matplotlib.pyplot.plot()keyword properties, optional) – Additional keywords passed to matplotlib to specify line properties.grid (bool) – If True, plot grid lines on gain and phase plots. Default is set by config.defaults[‘freqplot.grid’].
initial_phase (float) – Set the reference phase to use for the lowest frequency. If set, the initial phase of the Bode plot will be set to the value closest to the value specified. Units are in either degrees or radians, depending on the deg parameter. Default is -180 if wrap_phase is False, 0 if wrap_phase is True.
omega_limits (array_like of two values) – Set limits for plotted frequency range. If Hz=True the limits are in Hz otherwise in rad/s.
omega_num (int) – Number of samples to use for the frequeny range. Defaults to config.defaults[‘freqplot.number_of_samples’]. Ignore if data is not a list of systems.
plot (bool, optional) – (legacy) If given, bode_plot returns the legacy return values of magnitude, phase, and frequency. If False, just return the values with no plot.
rcParams (dict) – Override the default parameters used for generating plots. Default is set by config.default[‘freqplot.rcParams’].
wrap_phase (bool or float) – If wrap_phase is False (default), then the phase will be unwrapped so that it is continuously increasing or decreasing. If wrap_phase is True the phase will be restricted to the range [-180, 180) (or [
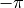 ,
, 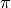 ) radians). If wrap_phase is specified
as a float, the phase will be offset by 360 degrees if it falls below
the specified value. Default value is False and can be set using
config.defaults[‘freqplot.wrap_phase’].
) radians). If wrap_phase is specified
as a float, the phase will be offset by 360 degrees if it falls below
the specified value. Default value is False and can be set using
config.defaults[‘freqplot.wrap_phase’].reset (The default values for Bode plot configuration parameters can be) –
dictionary (using the config.defaults) –
'bode'. (with module name) –
- Returns
lines – Array of Line2D objects for each line in the plot. The shape of the array matches the subplots shape and the value of the array is a list of Line2D objects in that subplot.
- Return type
array of Line2D
Notes
Starting with python-control version 0.10, bode_plot`returns an array of lines instead of magnitude, phase, and frequency. To recover the old behavior, call `bode_plot with plot=True, which will force the legacy values (mag, phase, omega) to be returned (with a warning). To obtain just the frequency response of a system (or list of systems) without plotting, use the
frequency_response()command.If a discrete time model is given, the frequency response is plotted along the upper branch of the unit circle, using the mapping
z = exp(1j * omega * dt)where omega ranges from 0 to pi/dt and dt is the discrete timebase. If timebase not specified (dt=True), dt is set to 1.
Examples
>>> G = ct.ss([[-1, -2], [3, -4]], [[5], [7]], [[6, 8]], [[9]]) >>> out = ct.bode_plot(G)