control.describing_function_response

control.describing_function_response(H, F, A, omega=None, refine=True, warn_nyquist=None, plot=False, check_kwargs=True, **kwargs)[source]

Compute the describing function response of a system.

This function uses describing function analysis to analyze a closed loop system consisting of a linear system with a static nonlinear function in the feedback path.

Parameters

H (LTI system) – Linear time-invariant (LTI) system (state space, transfer function, or FRD)
F (static nonlinear function) – A static nonlinearity, either a scalar function or a single-input, single-output, static input/output system.
A (list) – List of amplitudes to be used for the describing function plot.
omega (list, optional) – List of frequencies to be used for the linear system Nyquist curve.
warn_nyquist (bool, optional) – Set to True to turn on warnings generated by nyquist_plot or False to turn off warnings. If not set (or set to None), warnings are turned off if omega is specified, otherwise they are turned on.

Returns

response (DescribingFunctionResponse object) – Response object that contains the result of the describing function analysis. The following information can be retrieved from this object:
response.intersections (1D array of 2-tuples or None) – A list of all amplitudes and frequencies in which 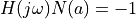$H(j\omega) N(a) = -1$ , where 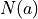$N(a)$ is the describing function associated with F, or None if there are no such points. Each pair represents a potential limit cycle for the closed loop system with amplitude given by the first value of the tuple and frequency given by the second value.

Examples

>>> H_simple = ct.tf([8], [1, 2, 2, 1])
>>> F_saturation = ct.saturation_nonlinearity(1)
>>> amp = np.linspace(1, 4, 10)
>>> response = ct.describing_function_response(H_simple, F_saturation, amp)
>>> response.intersections  
[(3.343844998258643, 1.4142293090899216)]
>>> lines = response.plot()