Describing functions
For nonlinear systems consisting of a feedback connection between a
linear system and a static nonlinearity, it is possible to obtain a
generalization of Nyquist’s stability criterion based on the idea of
describing functions. The basic concept involves approximating the
response of a static nonlinearity to an input 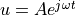 as an output
as an output 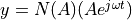 , where
, where 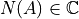 represents the (amplitude-dependent) gain and phase
associated with the nonlinearity.
represents the (amplitude-dependent) gain and phase
associated with the nonlinearity.
Stability analysis of a linear system 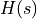 with a feedback
nonlinearity
with a feedback
nonlinearity 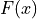 is done by looking for amplitudes
is done by looking for amplitudes 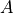 and frequencies
and frequencies 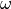 such that
such that
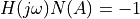
If such an intersection exists, it indicates that there may be a limit
cycle of amplitude 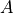 with frequency
with frequency 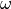 .
.
Describing function analysis is a simple method, but it is approximate because it assumes that higher harmonics can be neglected.
Module usage
The function describing_function() can be used to
compute the describing function of a nonlinear function:
N = ct.describing_function(F, A)
Stability analysis using describing functions is done by looking for
amplitudes  and frequencies :math`omega` such that
and frequencies :math`omega` such that
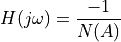
These points can be determined by generating a Nyquist plot in which
the transfer function 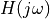 intersections the negative
reciprocal of the describing function
intersections the negative
reciprocal of the describing function 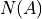 . The
. The
describing_function_response() function computes the
amplitude and frequency of any points of intersection:
response = ct.describing_function_response(H, F, amp_range[, omega_range])
response.intersections # frequency, amplitude pairs
A Nyquist plot showing the describing function and the intersections
with the Nyquist curve can be generated using response.plot(), which
calls the describing_function_plot() function.
Pre-defined nonlinearities
To facilitate the use of common describing functions, the following nonlinearity constructors are predefined:
friction_backlash_nonlinearity(b) # backlash nonlinearity with width b
relay_hysteresis_nonlinearity(b, c) # relay output of amplitude b with
# hysteresis of half-width c
saturation_nonlinearity(ub[, lb]) # saturation nonlinearity with upper
# bound and (optional) lower bound
Calling these functions will create an object F that can be used for describing function analysis. For example, to create a saturation nonlinearity:
F = ct.saturation_nonlinearity(1)
These functions use the
DescribingFunctionNonlinearity, which allows an
analytical description of the describing function.
Module classes and functions
Base class for nonlinear systems with a describing function. |
|
Backlash nonlinearity for describing function analysis. |
|
Relay w/ hysteresis nonlinearity for describing function analysis. |
|
|
Create saturation nonlinearity for use in describing function analysis. |