control.care

control.care(A, B, Q, R=None, S=None, E=None, stabilizing=True, method=None, _As='A', _Bs='B', _Qs='Q', _Rs='R', _Ss='S', _Es='E')[source]

Solves the continuous-time algebraic Riccati equation.

X, L, G = care(A, B, Q, R=None) solves

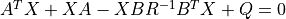
$A^T X + X A - X B R^{-1} B^T X + Q = 0$

where A and Q are square matrices of the same dimension. Further, Q and R are a symmetric matrices. If R is None, it is set to the identity matrix. The function returns the solution X, the gain matrix G = B^T X and the closed loop eigenvalues L, i.e., the eigenvalues of A - B G.

X, L, G = care(A, B, Q, R, S, E) solves the generalized continuous-time algebraic Riccati equation

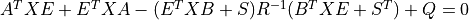
$A^T X E + E^T X A - (E^T X B + S) R^{-1} (B^T X E + S^T) + Q = 0$

where A, Q and E are square matrices of the same dimension. Further, Q and R are symmetric matrices. If R is None, it is set to the identity matrix. The function returns the solution X, the gain matrix G = R^-1 (B^T X E + S^T) and the closed loop eigenvalues L, i.e., the eigenvalues of A - B G , E.

Parameters

A, B, Q2D array_like: Input matrices for the Riccati equation.
R, S, E2D array_like, optional: Input matrices for generalized Riccati equation.
methodstr, optional: Set the method used for computing the result. Current methods are ‘slycot’ and ‘scipy’. If set to None (default), try ‘slycot’ first and then ‘scipy’.
stabilizingbool, optional: If method is ‘slycot’, unstabilized eigenvalues will be returned in the initial elements of L. Not supported for ‘scipy’.

Returns

X2D array (or matrix): Solution to the Riccati equation.
L1D array: Closed loop eigenvalues.
G2D array (or matrix): Gain matrix.