control.matlab.dare
- control.matlab.dare(A, B, Q, R, S=None, E=None, stabilizing=True, method=None, A_s='A', B_s='B', Q_s='Q', R_s='R', S_s='S', E_s='E')[source]
Solves the discrete-time algebraic Riccati equation.
X, L, G = dare(A, B, Q, R) solves
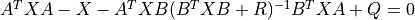
where A and Q are square matrices of the same dimension. Further, Q is a symmetric matrix. The function returns the solution X, the gain matrix G = (B^T X B + R)^-1 B^T X A and the closed loop eigenvalues L, i.e., the eigenvalues of A - B G.
X, L, G = dare(A, B, Q, R, S, E) solves the generalized discrete-time algebraic Riccati equation
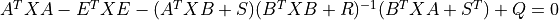
where A, Q and E are square matrices of the same dimension. Further, Q and R are symmetric matrices. If R is None, it is set to the identity matrix. The function returns the solution X, the gain matrix
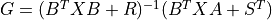 and the closed loop eigenvalues L,
i.e., the (generalized) eigenvalues of A - B G (with respect to E, if
specified).
and the closed loop eigenvalues L,
i.e., the (generalized) eigenvalues of A - B G (with respect to E, if
specified).- Parameters
A (2D arrays) – Input matrices for the Riccati equation
B (2D arrays) – Input matrices for the Riccati equation
Q (2D arrays) – Input matrices for the Riccati equation
R (2D arrays, optional) – Input matrices for generalized Riccati equation
S (2D arrays, optional) – Input matrices for generalized Riccati equation
E (2D arrays, optional) – Input matrices for generalized Riccati equation
method (str, optional) – Set the method used for computing the result. Current methods are ‘slycot’ and ‘scipy’. If set to None (default), try ‘slycot’ first and then ‘scipy’.
- Returns
X (2D array (or matrix)) – Solution to the Ricatti equation
L (1D array) – Closed loop eigenvalues
G (2D array (or matrix)) – Gain matrix