control.matlab.lqr¶
-
control.matlab.lqr(A, B, Q, R[, N])¶ Linear quadratic regulator design
The lqr() function computes the optimal state feedback controller that minimizes the quadratic cost
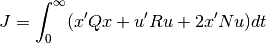
The function can be called with either 3, 4, or 5 arguments:
lqr(sys, Q, R)lqr(sys, Q, R, N)lqr(A, B, Q, R)lqr(A, B, Q, R, N)
where sys is an LTI object, and A, B, Q, R, and N are 2d arrays or matrices of appropriate dimension.
- Parameters
A (2D array) – Dynamics and input matrices
B (2D array) – Dynamics and input matrices
sys (LTI (StateSpace or TransferFunction)) – Linear I/O system
Q (2D array) – State and input weight matrices
R (2D array) – State and input weight matrices
N (2D array, optional) – Cross weight matrix
- Returns
K (2D array (or matrix)) – State feedback gains
S (2D array (or matrix)) – Solution to Riccati equation
E (1D array) – Eigenvalues of the closed loop system
See also
lqeNotes
The return type for 2D arrays depends on the default class set for state space operations. See
use_numpy_matrix().Examples
>>> K, S, E = lqr(sys, Q, R, [N]) >>> K, S, E = lqr(A, B, Q, R, [N])