control.StateSpace

class control.StateSpace(A, B, C, D[, dt])

Bases: NonlinearIOSystem, LTI

A class for representing state-space models.

The StateSpace class is used to represent state-space realizations of linear time-invariant (LTI) systems:

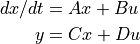
where u is the input, y is the output, and x is the state.

Parameters

• A (array_like) – System matrices of the appropriate dimensions.

• B (array_like) – System matrices of the appropriate dimensions.

• C (array_like) – System matrices of the appropriate dimensions.

• D (array_like) – System matrices of the appropriate dimensions.

• dt (None, True or float, optional) – System timebase. 0 (default) indicates continuous time, True indicates discrete time with unspecified sampling time, positive number is discrete time with specified sampling time, None indicates unspecified timebase (either continuous or discrete time).

ninputs, noutputs, nstates

Number of input, output and state variables.

Type

int

A, B, C, D

System matrices defining the input/output dynamics.

Type

2D arrays

dt

System timebase. 0 (default) indicates continuous time, True indicates discrete time with unspecified sampling time, positive number is discrete time with specified sampling time, None indicates unspecified timebase (either continuous or discrete time).

Type

None, True or float

Notes

The main data members in the StateSpace class are the A, B, C, and D matrices. The class also keeps track of the number of states (i.e., the size of A).

A discrete time system is created by specifying a nonzero ‘timebase’, dt when the system is constructed:

• dt = 0: continuous time system (default)

• dt > 0: discrete time system with sampling period ‘dt’

• dt = True: discrete time with unspecified sampling period

• dt = None: no timebase specified

Systems must have compatible timebases in order to be combined. A discrete time system with unspecified sampling time (dt = True) can be combined with a system having a specified sampling time; the result will be a discrete time system with the sample time of the latter system. Similarly, a system with timebase None can be combined with a system having any timebase; the result will have the timebase of the latter system. The default value of dt can be changed by changing the value of control.config.defaults['control.default_dt'].

A state space system is callable and returns the value of the transfer function evaluated at a point in the complex plane. See __call__() for a more detailed description.

Subsystems corresponding to selected input/output pairs can be created by indexing the state space system:

subsys = sys[output_spec, input_spec]

The input and output specifications can be single integers, lists of integers, or slices. In addition, the strings representing the names of the signals can be used and will be replaced with the equivalent signal offsets. The subsystem is created by truncating the inputs and outputs, but leaving the full set of system states.

StateSpace instances have support for IPython LaTeX output, intended for pretty-printing in Jupyter notebooks. The LaTeX output can be configured using control.config.defaults[‘statesp.latex_num_format’] and control.config.defaults[‘statesp.latex_repr_type’]. The LaTeX output is tailored for MathJax, as used in Jupyter, and may look odd when typeset by non-MathJax LaTeX systems.

control.config.defaults[‘statesp.latex_num_format’] is a format string fragment, specifically the part of the format string after ‘{:’ used to convert floating-point numbers to strings. By default it is ‘.3g’.

control.config.defaults[‘statesp.latex_repr_type’] must either be ‘partitioned’ or ‘separate’. If ‘partitioned’, the A, B, C, D matrices are shown as a single, partitioned matrix; if ‘separate’, the matrices are shown separately.

Methods

append	Append a second model to the present model.
bandwidth	Evaluate the bandwidth of the LTI system for a given dB drop.
copy	Make a copy of an input/output system
damp	Natural frequency, damping ratio of system poles
dcgain	Return the zero-frequency gain
dynamics	Compute the dynamics of the system
feedback	Feedback interconnection between two LTI systems.
find_input	Find the index for an input given its name (None if not found)
find_inputs	Return list of indices matching input spec (None if not found)
find_output	Find the index for an output given its name (None if not found)
find_outputs	Return list of indices matching output spec (None if not found)
find_state	Find the index for a state given its name (None if not found)
find_states	Return list of indices matching state spec (None if not found)
freqresp	(deprecated) Evaluate transfer function at complex frequencies.
frequency_response	Evaluate the linear time-invariant system at an array of angular frequencies.
horner	Evaluate system's transfer function at complex frequency using Laub's or Horner's method.
isctime	Check to see if a system is a continuous-time system.
isdtime	Check to see if a system is a discrete-time system
ispassive
issiso	Check to see if a system is single input, single output.
lft	Return the Linear Fractional Transformation.
linearize	Linearize an input/output system at a given state and input.
minreal	Calculate a minimal realization, removes unobservable and uncontrollable states
output	Compute the output of the system
poles	Compute the poles of a state space system.
returnScipySignalLTI	Return a list of a list of scipy.signal.lti objects.
sample	Convert a continuous time system to discrete time
set_inputs	Set the number/names of the system inputs.
set_outputs	Set the number/names of the system outputs.
set_states	Set the number/names of the system states.
slycot_laub	Evaluate system's transfer function at complex frequency using Laub's method from Slycot.
update_names	Update signal and system names for an I/O system.
zeros	Compute the zeros of a state space system.

A

Dynamics matrix.

B

Input matrix.

C

Output matrix.

D

Direct term.

__add__(other)

Add two LTI systems (parallel connection).

__call__(x, squeeze=None, warn_infinite=True)

Evaluate system’s frequency response at complex frequencies.

Returns the complex frequency response sys(x) where x is s for continuous-time systems and z for discrete-time systems.

To evaluate at a frequency omega in radians per second, enter x = omega * 1j, for continuous-time systems, or x = exp(1j * omega * dt) for discrete-time systems. Or use StateSpace.frequency_response().

Parameters

• x (complex or complex 1D array_like) – Complex frequencies

• squeeze (bool, optional) – If squeeze=True, remove single-dimensional entries from the shape of the output even if the system is not SISO. If squeeze=False, keep all indices (output, input and, if omega is array_like, frequency) even if the system is SISO. The default value can be set using config.defaults[‘control.squeeze_frequency_response’].

• warn_infinite (bool, optional) – If set to False, don’t warn if frequency response is infinite.

Returns

fresp – The frequency response of the system. If the system is SISO and squeeze is not True, the shape of the array matches the shape of omega. If the system is not SISO or squeeze is False, the first two dimensions of the array are indices for the output and input and the remaining dimensions match omega. If squeeze is True then single-dimensional axes are removed.

Return type

complex ndarray

__getitem__(key)

Array style access

__mul__(other)

Multiply two LTI objects (serial connection).

__neg__()

Negate a state space system.

__radd__(other)

Right add two LTI systems (parallel connection).

__rmul__(other)

Right multiply two LTI objects (serial connection).

__rsub__(other)

Right subtract two LTI systems.

__sub__(other)

Subtract two LTI systems.

__truediv__(other)

Division of state space systems by TFs, FRDs, scalars, and arrays

append(other)

Append a second model to the present model.

The second model is converted to state-space if necessary, inputs and outputs are appended and their order is preserved

bandwidth(dbdrop=-3)

Evaluate the bandwidth of the LTI system for a given dB drop.

Evaluate the first frequency that the response magnitude is lower than DC gain by dbdrop dB.

Parameters

dpdrop (float, optional) – A strictly negative scalar in dB (default = -3) defines the amount of gain drop for deciding bandwidth.

Returns

bandwidth – The first frequency (rad/time-unit) where the gain drops below dbdrop of the dc gain of the system, or nan if the system has infinite dc gain, inf if the gain does not drop for all frequency

Return type

ndarray

Raises

• TypeError – if ‘sys’ is not an SISO LTI instance

• ValueError – if ‘dbdrop’ is not a negative scalar

copy(name=None, use_prefix_suffix=True)

Make a copy of an input/output system

A copy of the system is made, with a new name. The name keyword can be used to specify a specific name for the system. If no name is given and use_prefix_suffix is True, the name is constructed by prepending config.defaults[‘iosys.duplicate_system_name_prefix’] and appending config.defaults[‘iosys.duplicate_system_name_suffix’]. Otherwise, a generic system name of the form sys[<id>] is used, where <id> is based on an internal counter.

damp()

Natural frequency, damping ratio of system poles

Returns

• wn (array) – Natural frequency for each system pole

• zeta (array) – Damping ratio for each system pole

• poles (array) – System pole locations

dcgain(warn_infinite=False)

Return the zero-frequency gain

The zero-frequency gain of a continuous-time state-space system is given by:

and of a discrete-time state-space system by:

Parameters

warn_infinite (bool, optional) – By default, don’t issue a warning message if the zero-frequency gain is infinite. Setting warn_infinite to generate the warning message.

Returns

gain – Array or scalar value for SISO systems, depending on config.defaults[‘control.squeeze_frequency_response’]. The value of the array elements or the scalar is either the zero-frequency (or DC) gain, or inf, if the frequency response is singular.

For real valued systems, the empty imaginary part of the complex zero-frequency response is discarded and a real array or scalar is returned.

Return type

(noutputs, ninputs) ndarray or scalar

dynamics(t, x, u=None, params=None)

Compute the dynamics of the system

Given input u and state x, returns the dynamics of the state-space system. If the system is continuous, returns the time derivative dx/dt

dx/dt = A x + B u

where A and B are the state-space matrices of the system. If the system is discrete-time, returns the next value of x:

x[t+dt] = A x[t] + B u[t]

The inputs x and u must be of the correct length for the system.

The first argument t is ignored because StateSpace systems are time-invariant. It is included so that the dynamics can be passed to numerical integrators, such as scipy.integrate.solve_ivp() and for consistency with IOSystem systems.

Parameters

• t (float (ignored)) – time

• x (array_like) – current state

• u (array_like (optional)) – input, zero if omitted

Returns

dx/dt or x[t+dt]

Return type

ndarray

feedback(other=1, sign=-1)

Feedback interconnection between two LTI systems.

find_input(name)

Find the index for an input given its name (None if not found)

find_inputs(name_list)

Return list of indices matching input spec (None if not found)

find_output(name)

Find the index for an output given its name (None if not found)

find_outputs(name_list)

Return list of indices matching output spec (None if not found)

find_state(name)

Find the index for a state given its name (None if not found)

find_states(name_list)

Return list of indices matching state spec (None if not found)

freqresp(omega)

(deprecated) Evaluate transfer function at complex frequencies.

frequency_response(omega=None, squeeze=None)

Evaluate the linear time-invariant system at an array of angular frequencies.

For continuous time systems, computes the frequency response as

G(j*omega) = mag * exp(j*phase)

For discrete time systems, the response is evaluated around the unit circle such that

G(exp(j*omega*dt)) = mag * exp(j*phase).

In general the system may be multiple input, multiple output (MIMO), where m = self.ninputs number of inputs and p = self.noutputs number of outputs.

Parameters

• omega (float or 1D array_like) – A list, tuple, array, or scalar value of frequencies in radians/sec at which the system will be evaluated.

• squeeze (bool, optional) – If squeeze=True, remove single-dimensional entries from the shape of the output even if the system is not SISO. If squeeze=False, keep all indices (output, input and, if omega is array_like, frequency) even if the system is SISO. The default value can be set using config.defaults[‘control.squeeze_frequency_response’].

Returns

response – Frequency response data object representing the frequency response. This object can be assigned to a tuple using

mag, phase, omega = response

where mag is the magnitude (absolute value, not dB or log10) of the system frequency response, phase is the wrapped phase in radians of the system frequency response, and omega is the (sorted) frequencies at which the response was evaluated. If the system is SISO and squeeze is not True, magnitude and phase are 1D, indexed by frequency. If the system is not SISO or squeeze is False, the array is 3D, indexed by the output, input, and, if omega is array_like, frequency. If squeeze is True then single-dimensional axes are removed.

Return type

FrequencyResponseData

horner(x, warn_infinite=True)

Evaluate system’s transfer function at complex frequency using Laub’s or Horner’s method.

Evaluates sys(x) where x is s for continuous-time systems and z for discrete-time systems.

Expects inputs and outputs to be formatted correctly. Use sys(x) for a more user-friendly interface.

Parameters

x (complex array_like or complex) – Complex frequencies

Returns

output – Frequency response

Return type

(self.noutputs, self.ninputs, len(x)) complex ndarray

Notes

Attempts to use Laub’s method from Slycot library, with a fall-back to python code.

isctime(strict=False)

Check to see if a system is a continuous-time system.

Parameters

• sys (Named I/O system) – System to be checked

• strict (bool, optional) – If strict is True, make sure that timebase is not None. Default is False.

isdtime(strict=False)

Check to see if a system is a discrete-time system

Parameters

strict (bool, optional) – If strict is True, make sure that timebase is not None. Default is False.

issiso()

Check to see if a system is single input, single output.

lft(other, nu=-1, ny=-1)

Return the Linear Fractional Transformation.

A definition of the LFT operator can be found in Appendix A.7, page 512 in the 2nd Edition, Multivariable Feedback Control by Sigurd Skogestad.

An alternative definition can be found here: https://www.mathworks.com/help/control/ref/lft.html

Parameters

• other (LTI) – The lower LTI system

• ny (int, optional) – Dimension of (plant) measurement output.

• nu (int, optional) – Dimension of (plant) control input.

linearize(x0, u0=None, t=0, params=None, eps=1e-06, copy_names=False, **kwargs)

Linearize an input/output system at a given state and input.

Return the linearization of an input/output system at a given operating point (or state and input value) as a StateSpace system. See linearize() for complete documentation.

minreal(tol=0.0)

Calculate a minimal realization, removes unobservable and uncontrollable states

ninputs

Number of system inputs.

noutputs

Number of system outputs.

nstates

Number of system states.

output(t, x, u=None, params=None)

Compute the output of the system

Given input u and state x, returns the output y of the state-space system:

y = C x + D u

where A and B are the state-space matrices of the system.

The first argument t is ignored because StateSpace systems are time-invariant. It is included so that the dynamics can be passed to most numerical integrators, such as scipy’s integrate.solve_ivp and for consistency with IOSystem systems.

The inputs x and u must be of the correct length for the system.

Parameters

• t (float (ignored)) – time

• x (array_like) – current state

• u (array_like (optional)) – input (zero if omitted)

Returns

y

Return type

ndarray

poles()

Compute the poles of a state space system.

returnScipySignalLTI(strict=True)

Return a list of a list of scipy.signal.lti objects.

For instance,

>>> out = ssobject.returnScipySignalLTI()               
>>> out[3][5]                                           

is a scipy.signal.lti object corresponding to the transfer function from the 6th input to the 4th output.

Parameters

strict (bool, optional) –

True (default):

The timebase ssobject.dt cannot be None; it must be continuous (0) or discrete (True or > 0).

False:

If ssobject.dt is None, continuous time scipy.signal.lti objects are returned.

Returns

out – continuous time (inheriting from scipy.signal.lti) or discrete time (inheriting from scipy.signal.dlti) SISO objects

Return type

list of list of scipy.signal.StateSpace

sample(Ts, method='zoh', alpha=None, prewarp_frequency=None, name=None, copy_names=True, **kwargs)

Convert a continuous time system to discrete time

Creates a discrete-time system from a continuous-time system by sampling. Multiple methods of conversion are supported.

Parameters

• Ts (float) – Sampling period

• method ({"gbt", "bilinear", "euler", "backward_diff", "zoh"}) –

  Which method to use:

  • gbt: generalized bilinear transformation

  • bilinear: Tustin’s approximation (“gbt” with alpha=0.5)

  • euler: Euler (or forward differencing) method (“gbt” with alpha=0)

  • backward_diff: Backwards differencing (“gbt” with alpha=1.0)

  • zoh: zero-order hold (default)

• alpha (float within [0, 1]) – The generalized bilinear transformation weighting parameter, which should only be specified with method=”gbt”, and is ignored otherwise

• prewarp_frequency (float within [0, infinity)) – The frequency [rad/s] at which to match with the input continuous- time system’s magnitude and phase (the gain=1 crossover frequency, for example). Should only be specified with method=’bilinear’ or ‘gbt’ with alpha=0.5 and ignored otherwise.

• name (string, optional) – Set the name of the sampled system. If not specified and if copy_names is False, a generic name <sys[id]> is generated with a unique integer id. If copy_names is True, the new system name is determined by adding the prefix and suffix strings in config.defaults[‘iosys.sampled_system_name_prefix’] and config.defaults[‘iosys.sampled_system_name_suffix’], with the default being to add the suffix ‘$sampled’.

• copy_names (bool, Optional) – If True, copy the names of the input signals, output signals, and states to the sampled system.

• inputs (int, list of str or None, optional) – Description of the system inputs. If not specified, the origional system inputs are used. See InputOutputSystem for more information.

• outputs (int, list of str or None, optional) – Description of the system outputs. Same format as inputs.

• states (int, list of str, or None, optional) – Description of the system states. Same format as inputs.

Returns

sysd – Discrete-time system, with sampling rate Ts

Return type

StateSpace

Notes

Uses scipy.signal.cont2discrete()

Examples

>>> G = ct.ss(0, 1, 1, 0)
>>> sysd = G.sample(0.5, method='bilinear')

set_inputs(inputs, prefix='u')

Set the number/names of the system inputs.

Parameters

• inputs (int, list of str, or None) – Description of the system inputs. This can be given as an integer count or as a list of strings that name the individual signals. If an integer count is specified, the names of the signal will be of the form u[i] (where the prefix u can be changed using the optional prefix parameter).

• prefix (string, optional) – If inputs is an integer, create the names of the states using the given prefix (default = ‘u’). The names of the input will be of the form prefix[i].

set_outputs(outputs, prefix='y')

Set the number/names of the system outputs.

Parameters

• outputs (int, list of str, or None) – Description of the system outputs. This can be given as an integer count or as a list of strings that name the individual signals. If an integer count is specified, the names of the signal will be of the form u[i] (where the prefix u can be changed using the optional prefix parameter).

• prefix (string, optional) – If outputs is an integer, create the names of the states using the given prefix (default = ‘y’). The names of the input will be of the form prefix[i].

set_states(states, prefix='x')

Set the number/names of the system states.

Parameters

• states (int, list of str, or None) – Description of the system states. This can be given as an integer count or as a list of strings that name the individual signals. If an integer count is specified, the names of the signal will be of the form u[i] (where the prefix u can be changed using the optional prefix parameter).

• prefix (string, optional) – If states is an integer, create the names of the states using the given prefix (default = ‘x’). The names of the input will be of the form prefix[i].

slycot_laub(x)

Evaluate system’s transfer function at complex frequency using Laub’s method from Slycot.

Expects inputs and outputs to be formatted correctly. Use sys(x) for a more user-friendly interface.

Parameters

x (complex array_like or complex) – Complex frequency

Returns

output – Frequency response

Return type

(number_outputs, number_inputs, len(x)) complex ndarray

property states

Deprecated attribute; use nstates instead.

The state attribute was used to store the number of states for : a state space system. It is no longer used. If you need to access the number of states, use nstates.

update_names([name, inputs, outputs, states])

Update signal and system names for an I/O system.

Parameters

• name (str, optional) – New system name.

• inputs (list of str, int, or None, optional) – List of strings that name the individual input signals. If given as an integer or None, signal names default to the form u[i]. See InputOutputSystem for more information.

• outputs (list of str, int, or None, optional) – Description of output signals; defaults to y[i].

• states (int, list of str, int, or None, optional) – Description of system states; defaults to x[i].

zeros()

Compute the zeros of a state space system.