Library conventions
The python-control library uses a set of standard conventions for the way that different types of standard information used by the library. Throughout this manual, we assume the control package has been imported as ct.
LTI system representation
Linear time invariant (LTI) systems are represented in python-control in state space, transfer function, or frequency response data (FRD) form. Most functions in the toolbox will operate on any of these data types, and functions for converting between compatible types are provided.
State space systems
The StateSpace class is used to represent state-space realizations
of linear time-invariant (LTI) systems:
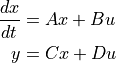
where u is the input, y is the output, and x is the state.
To create a state space system, use the ss() function:
sys = ct.ss(A, B, C, D)
State space systems can be manipulated using standard arithmetic operations
as well as the feedback(), parallel(), and series()
function. A full list of functions can be found in Function reference.
Transfer functions
The TransferFunction class is used to represent input/output
transfer functions
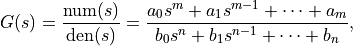
where n is generally greater than or equal to m (for a proper transfer function).
To create a transfer function, use the tf() function:
sys = ct.tf(num, den)
Transfer functions can be manipulated using standard arithmetic operations
as well as the feedback(), parallel(), and series()
function. A full list of functions can be found in Function reference.
FRD (frequency response data) systems
The FrequencyResponseData (FRD) class is used to represent systems in
frequency response data form.
The main data members are omega and fresp, where omega is a 1D array with the frequency points of the response, and fresp is a 3D array, with the first dimension corresponding to the output index of the FRD, the second dimension corresponding to the input index, and the 3rd dimension corresponding to the frequency points in omega.
FRD systems have a somewhat more limited set of functions that are available, although all of the standard algebraic manipulations can be performed.
The FRD class is also used as the return type for the
frequency_response() function (and the equivalent method for the
StateSpace and TransferFunction classes). This
object can be assigned to a tuple using:
mag, phase, omega = response
where mag is the magnitude (absolute value, not dB or log10) of the
system frequency response, phase is the wrapped phase in radians of
the system frequency response, and omega is the (sorted) frequencies
at which the response was evaluated. If the system is SISO and the
squeeze argument to frequency_response() is not True,
magnitude and phase are 1D, indexed by frequency. If the system
is not SISO or squeeze is False, the array is 3D, indexed by the
output, input, and frequency. If squeeze is True then
single-dimensional axes are removed. The processing of the squeeze
keyword can be changed by calling the response function with a new
argument:
mag, phase, omega = response(squeeze=False)
Discrete time systems
A discrete time system is created by specifying a nonzero ‘timebase’, dt. The timebase argument can be given when a system is constructed:
dt = 0: continuous time system (default)
dt > 0: discrete time system with sampling period ‘dt’
dt = True: discrete time with unspecified sampling period
dt = None: no timebase specified
Only the StateSpace, TransferFunction, and
InputOutputSystem classes allow explicit representation of
discrete time systems.
Systems must have compatible timebases in order to be combined. A discrete
time system with unspecified sampling time (dt = True) can be combined with
a system having a specified sampling time; the result will be a discrete time
system with the sample time of the latter system. Similarly, a system with
timebase None can be combined with a system having a specified timebase; the
result will have the timebase of the latter system. For continuous time
systems, the sample_system() function or the StateSpace.sample()
and TransferFunction.sample() methods can be used to create a discrete
time system from a continuous time system. See
Utility functions and conversions. The default value of dt can be changed by
changing the value of control.config.defaults[‘control.default_dt’].
Simulating LTI systems
A number of functions are available for computing the output (and state) response of an LTI systems:
|
Compute the initial condition response for a linear system. |
|
Compute the step response for a linear system. |
|
Compute the impulse response for a linear system. |
|
Compute the output of a linear system given the input. |
Each of these functions returns a TimeResponseData object
that contains the data for the time response (described in more detail
in the next section).
The forced_response() system is the most general and allows by
the zero initial state response to be simulated as well as the
response from a non-zero initial condition.
In addition the input_output_response() function, which handles
simulation of nonlinear systems and interconnected systems, can be
used. For an LTI system, results are generally more accurate using
the LTI simulation functions above. The input_output_response()
function is described in more detail in the Input/output systems section.
Time series data
A variety of functions in the library return time series data: sequences of
values that change over time. A common set of conventions is used for
returning such data: columns represent different points in time, rows are
different components (e.g., inputs, outputs or states). For return
arguments, an array of times is given as the first returned argument,
followed by one or more arrays of variable values. This convention is used
throughout the library, for example in the functions
forced_response(), step_response(), impulse_response(),
and initial_response().
Note
The convention used by python-control is different from the convention used in the scipy.signal library. In Scipy’s convention the meaning of rows and columns is interchanged. Thus, all 2D values must be transposed when they are used with functions from scipy.signal.
The time vector is a 1D array with shape (n, ):
T = [t1, t2, t3, ..., tn ]
Input, state, and output all follow the same convention. Columns are different points in time, rows are different components:
U = [[u1(t1), u1(t2), u1(t3), ..., u1(tn)]
[u2(t1), u2(t2), u2(t3), ..., u2(tn)]
...
...
[ui(t1), ui(t2), ui(t3), ..., ui(tn)]]
(and similarly for X, Y). So, U[:, 2] is the system’s input at the third point in time; and U[1] or U[1, :] is the sequence of values for the system’s second input.
When there is only one row, a 1D object is accepted or returned, which adds convenience for SISO systems:
The initial conditions are either 1D, or 2D with shape (j, 1):
X0 = [[x1]
[x2]
...
...
[xj]]
Functions that return time responses (e.g., forced_response(),
impulse_response(), input_output_response(),
initial_response(), and step_response()) return a
TimeResponseData object that contains the data for the time
response. These data can be accessed via the
time, outputs,
states and inputs
properties:
sys = ct.rss(4, 1, 1)
response = ct.step_response(sys)
plot(response.time, response.outputs)
The dimensions of the response properties depend on the function being
called and whether the system is SISO or MIMO. In addition, some time
response function can return multiple “traces” (input/output pairs),
such as the step_response() function applied to a MIMO system,
which will compute the step response for each input/output pair. See
TimeResponseData for more details.
The time response functions can also be assigned to a tuple, which extracts the time and output (and optionally the state, if the return_x keyword is used). This allows simple commands for plotting:
t, y = ct.step_response(sys)
plot(t, y)
The output of a MIMO LTI system can be plotted like this:
t, y = ct.forced_response(sys, t, u)
plot(t, y[0], label='y_0')
plot(t, y[1], label='y_1')
The convention also works well with the state space form of linear systems. If D is the feedthrough matrix (2D array) of a linear system, and U is its input (array), then the feedthrough part of the system’s response, can be computed like this:
ft = D @ U
Finally, the to_pandas() function can be used to create a pandas dataframe:
df = response.to_pandas()
The column labels for the data frame are time and the labels for the input,
output, and state signals (u[i], y[i], and x[i] by default, but these
can be changed using the inputs, outputs, and states keywords when
constructing the system, as described in ss(), tf(), and other
system creation function. Note that when exporting to pandas, “rows” in the
data frame correspond to time and “cols” (DataSeries) correspond to signals.
Package configuration parameters
The python-control library can be customized to allow for different default values for selected parameters. This includes the ability to set the style for various types of plots and establishing the underlying representation for state space matrices.
To set the default value of a configuration variable, set the appropriate element of the control.config.defaults dictionary:
ct.config.defaults['module.parameter'] = value
The ~control.config.set_defaults function can also be used to set multiple configuration parameters at the same time:
ct.config.set_defaults('module', param1=val1, param2=val2, ...]
Finally, there are also functions available set collections of variables based on standard configurations.
Selected variables that can be configured, along with their default values:
freqplot.dB (False): Bode plot magnitude plotted in dB (otherwise powers of 10)
freqplot.deg (True): Bode plot phase plotted in degrees (otherwise radians)
freqplot.Hz (False): Bode plot frequency plotted in Hertz (otherwise rad/sec)
freqplot.grid (True): Include grids for magnitude and phase plots
freqplot.number_of_samples (1000): Number of frequency points in Bode plots
freqplot.feature_periphery_decade (1.0): How many decades to include in the frequency range on both sides of features (poles, zeros).
statesp.default_dt and xferfcn.default_dt (None): set the default value of dt when constructing new LTI systems
statesp.remove_useless_states (True): remove states that have no effect on the input-output dynamics of the system
Additional parameter variables are documented in individual functions
Functions that can be used to set standard configurations:
Reset configuration values to their default (initial) values. |
|
Use Feedback Systems (FBS) compatible settings. |
|
Use MATLAB compatible configuration settings. |
|
|
Sets the defaults to whatever they were in a given release. |